Generative modeling is currently one of the most thrilling domains in deep learning research. Traditional models like Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs) have already demonstrated impressive capabilities in synthetically generating realistic data, such as images and text. However, diffusion models is swiftly gaining prominence as a powerful model in the arena of high-quality and stable generative modeling. This blog explores diffusion models, examining their operational mechanisms, architectural designs, training processes, sampling methods, and the key advantages that position them at the forefront of generative AI.

The foundations of diffusion models were introduced in papers by Sohl-Dickstein et al. and Ho et al.

How Do Diffusion Models Work?

Diffusion models function on a principal strategy of training a model to reverse a gradual process of data corruption, transitioning from a clean data point to pure noise and then back to clean data point.

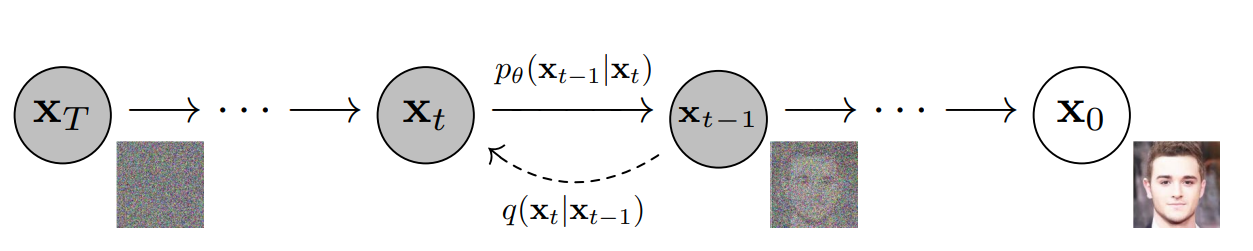asd Image Source: Ho et al.

Forward Diffusion Process

This corruption is executed through the forward diffusion process. It is characterized by the iterative addition of small quantities of Gaussian noise to the data \(x_0\) over \(T\) discrete time steps. This process is mathematically expressed as:

\[ x_t = \sqrt{1 - \beta_t} \times x_{t-1} + \sqrt{\beta_t} \times \epsilon \]

In this equation, \(x_t\) represents the partially corrupted data at time \(t\), \(\beta_t\) is the noise parameter that controls variance, and \(\epsilon\) signifies Gaussian noise. As \(t\) increases, \(\beta_t\) is progressively annealed from a lower to higher value, methodically erasing the structure in \(x_0\) until it becomes unrecognizable noise \(x_T\).

Reverse Diffusion Process

The core of the diffusion model is a neural network trained to precisely reverse this forward process. It accepts \(x_t\) as input and predicts \(x_{t-1}\), the less noisy version from the preceding step. By consecutively predicting each step in reverse, the model systematically denoises \(x_T\) back into a clear sample \(x_0\).

A critical aspect of this training involves denoising score matching, where the model aims to predict the gradient of the log-probability of \(x_{t-1}\) given \(x_t\). This approach, relying on noise data from the forward process, is key to the model’s stable training.

Diffusion Model Architectures

Diffusion models commonly utilize convolutional neural networks, particularly U-Net architectures. The contracting and expanding paths in U-Nets facilitate both local and global attention to the noise, yielding high-quality outputs.

Conditional variants of these models integrate class embeddings at intermediate layers, allowing for controlled sampling of specific classes of data, like images of diverse objects.

Training Process

Diffusion models are distinct in that they are trained using a denoising score matching loss rather than a standard likelihood loss. During training, the model is exposed only to artificially noised data from the forward process, never to clean data. This approach enables large-scale stable training and mitigates issues like mode collapse, common in likelihood-based models such as GANs, especially on diverse datasets. The iterative training on noise data endows diffusion models with robust generative capabilities.

Sampling Methods

To generate samples from a trained diffusion model, one starts with pure noise \(x_T\) and progressively predicts \(x_{T-1}\), \(x_{T-2}\), and so on, using the model’s predicted denoising score at each step.

The number of sampling steps is crucial; approximately 1000 steps can recover fine details clearly, whereas fewer steps might result in distorted outputs. Post-processing techniques, such as upscaling, can further enhance the quality of the samples.

Advantages Over Other Models

Diffusion models offer several advantages over existing generative models, making them a promising new direction in the field:

  • Sample Quality: The iterative denoising process facilitates the creation of high-resolution, clear samples that effectively capture the complexity of data.
  • Training Stability: Exposure to only artificial noise data prevents collapse issues and enables scalable training.
  • Flexible Control: Class-conditional variants offer significant control over sampling specific data types.
  • Parallelizable Sampling: Each step in the sampling process can be efficiently parallelized across GPUs.

Current Limitations

Despite their advantages, diffusion models do face certain limitations:

  • Sampling is computationally intensive, requiring hundreds of passes.
  • Numerous hyperparameters related to the noise schedule needs careful tuning.
  • Class-conditional guidance is limited compared to the desired level of control.

The Future of Generative AI

Diffusion models are exceptionally promising as generative models due to both sample quality and training stability. With rapid innovations in architecture, hyperparameters, and sampling techniques, they represent the new frontier in generative modeling with vast potentials still to be unlocked. As research continues, we can expect diffusion models to become even more powerful and flexible generative tools.